mediodía · exterior

Marta me envió este video. Así me queda cuando lo intento:

espiral a mano

No tengo el pulso para eso.

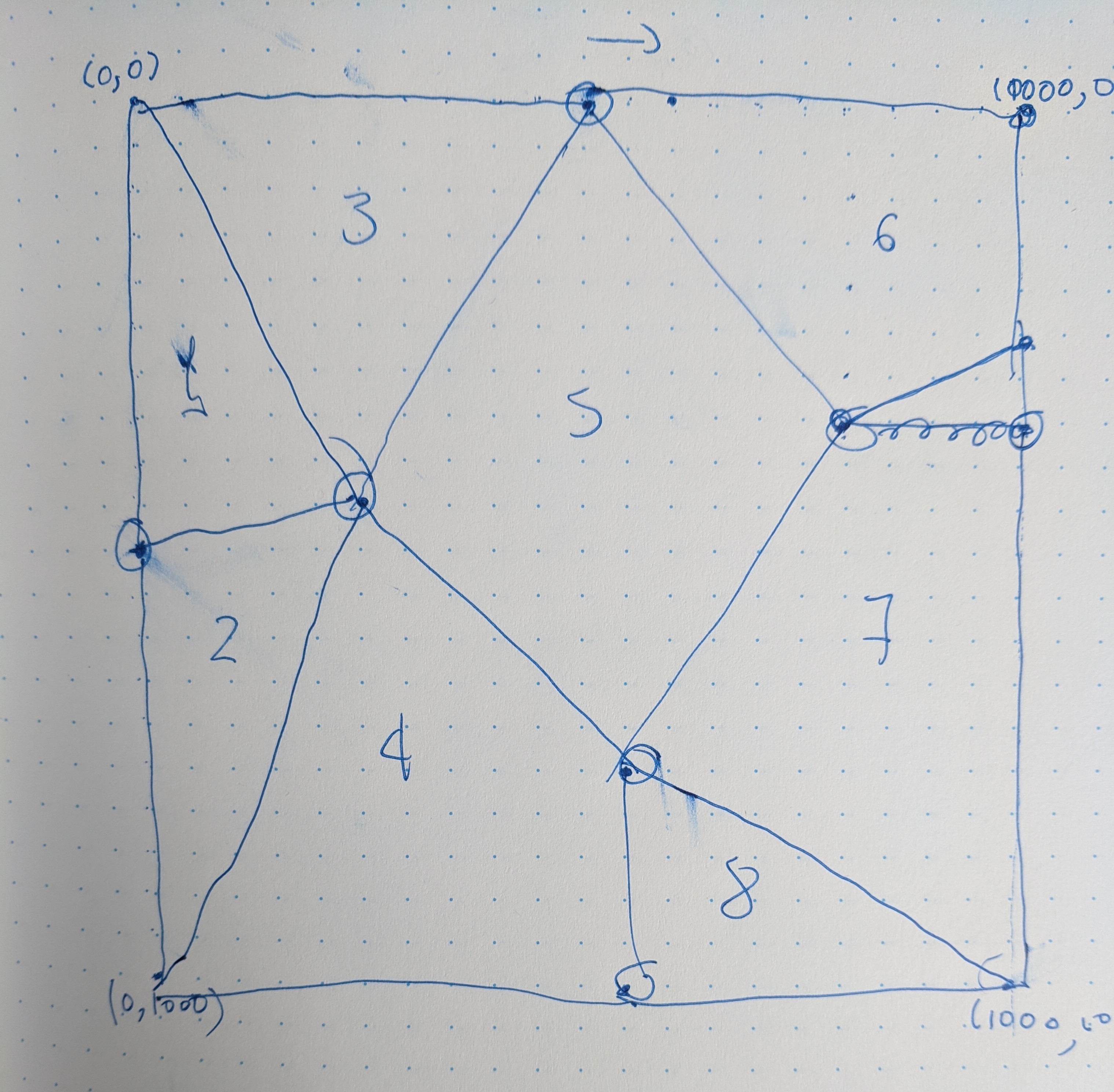
Anoche intenté armar algo para hacer esos diseños de espirales en el computador. Asumamos que tenemos un polígono definido por sus vértices (en un orden para dibujarlo.) Digamos un cuadrado:

 
polygon = [[0, 0], [1000, 0], [1000, 1000], [0, 1000]]

Las piezas fundamentales son estas dos funciones:

 
import numpy as np

def next_point(q, r, fraction):
    return q + fraction * (r - q)

def spiral(polygon, N=360, fraction=0.1):
    sequence = [np.array(x) for x in polygon + [polygon[0]]]
    total_points = len(sequence)
    for i in range(N):
        sequence.append(
            next_point(
                sequence[-(total_points - 1)], 
                sequence[-(total_points - 2)], 
                fraction=fraction
            )
        )
    return sequence

Para dibujarlas, podemos usar ipycanvas otra vez. Es pesado pero práctico para dibujos así:

# Assuming an appropriate ipycanvas canvas is available.  
def plot_spiral(canvas, sequence):
    canvas.begin_path()
    canvas.move_to(*sequence[0])
    for point in sequence[1:]:
        canvas.line_to(*point)
    canvas.stroke()

Por ejemplo, así se ve nuestro polígono original con los cuatro primeros trazos de la espiral:

from ipycanvas import Canvas

canvas = Canvas(width=1000, height=1000)
canvas.scale(1)    
canvas.fill_style = '#fdf3dc'
canvas.fill_rect(0, 0, 1000, 1000)
canvas.line_width = 0.3
plot_spiral(canvas, spiral(polygon, N=4))
canvas

textil 01010-00100

Y eso con 240 trazos:

canvas = Canvas(width=1000, height=1000)
canvas.scale(1)    
canvas.fill_style = '#fdf3dc'
canvas.fill_rect(0, 0, 1000, 1000)
canvas.line_width = 0.3
plot_spiral(canvas, spiral(polygon, N=240))
canvas

textil 01010-00100

Algo que vale la pena resaltar es que los polígonos deben ser definidos en orden, a menos que se busque este tipo de efectos:

polygon = [[0, 0], [0, 1000], [1000, 1000], [1000, 0]]

canvas = Canvas(width=1000, height=1000)
canvas.scale(1)    
canvas.fill_style = '#fdf3dc'
canvas.fill_rect(0, 0, 1000, 1000)
canvas.line_width = 0.3
plot_spiral(canvas, spiral(polygon, N=240))
canvas

textil 01010-00100

Me recuerdan manualidades con clavos e hilos de colores que hacía cuando era pequeño.

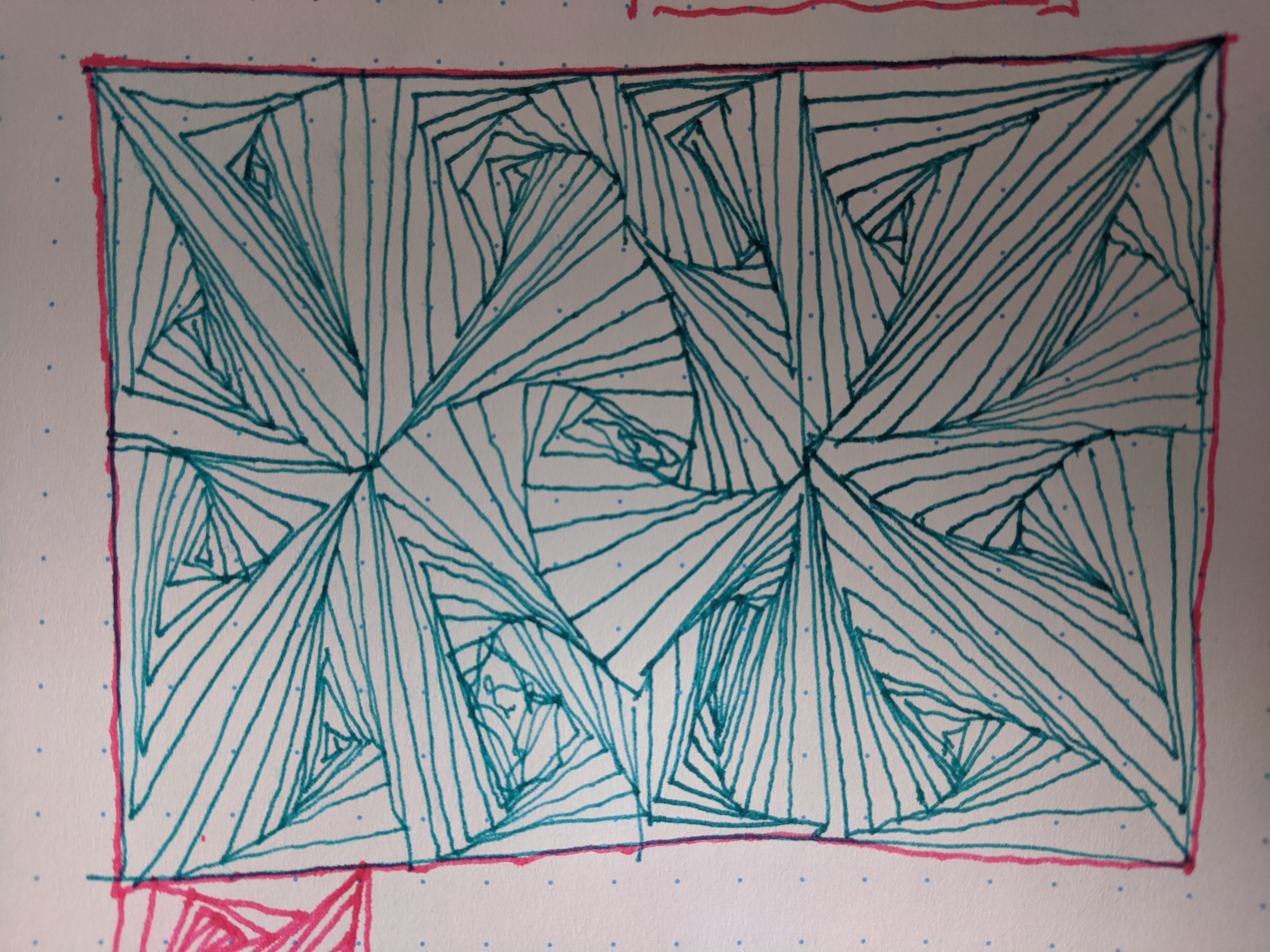
Después de resolver este problema, intenté armar diseños a mano y después codificarlos. Este fue uno:

textil 01010-00100

En código luce así:

polygons = [
    [(0, 0), (0, 500), (250, 450)],
    [(0, 500), (250, 450), (0, 1000)],
    [(0, 0), (250, 450), (600, 0)],
    [(250, 450), (0, 1000), (500, 1000), (500, 750)],
    [(600, 0), (250, 450), (500, 750), (800, 350)],
    [(600, 0), (800, 350), (1000, 250), (1000, 0)],
    [(500, 750), (800, 350), (1000, 250), (1000, 1000)],
    [(500, 750), (1000, 1000), (500, 1000)],
]

canvas = Canvas(width=1000, height=1000)
canvas.scale(1)    
canvas.fill_style = '#fdf3dc'
canvas.fill_rect(0, 0, 1000, 1000)
canvas.line_width = 0.3
for polygon in polygons:
    plot_spiral(canvas, spiral(polygon))
canvas

Y se ve así:

textil 01010-00100

Lo siguiente fue jugar con técnicas que permiten teselar el plano con polígonos convexos, por ejemplo la triangulación de Delaunay:

from scipy.spatial import Delaunay

np.random.seed(0)
main_vertices = [[0, 0], [0, 1000], [1000, 0], [1000, 1000]]
# 100 points randomly sampled from the square:
add_ons = np.random.uniform(150, 850, size=(100, 2)).tolist()
all_points = np.array(main_vertices + add_ons)

tri = Delaunay(all_points)

canvas = Canvas(width=1000, height=1000)
canvas.scale(1)    
canvas.fill_style = '#fdf3dc'
canvas.fill_rect(0, 0, 1000, 1000)
canvas.line_width = 0.1
for polygon in all_points[tri.simplices]:
    plot_spiral(canvas, spiral(polygon.tolist(), N=30))
canvas

Esto se ve así:

textil 01010-00100

Pero algo que no me gusta de las triangulaciones de Delaunay es que son, precisamente, triangulaciones. El diagrama de Voronoi (dual de la triangulación de Delaunay) genera teselaciones con polígonos convexos de diferentes números de lados (aunque sin mayor control, y se definen centroides en lugar de vértices de los polígonos):

from scipy.spatial import Voronoi

np.random.seed(3)
main_vertices = [[0, 0], [0, 1000], [1000, 0], [1000, 1000]]
add_ons = np.random.uniform(-100, 1100, size=(60, 2)).tolist()
all_points = np.array(main_vertices + add_ons)

vor = Voronoi(all_points)
voronoi_polygons = [[vor.vertices[z].tolist() for z in x] for x in vor.regions if x and all([y>=0 for y in x])]
voronoi_polygons = [x for x in voronoi_polygons if (np.array(x) > 0).all() and (np.array(x) < 1000).all()]

canvas = Canvas(width=1000, height=1000)
canvas.scale(1)    
canvas.fill_style = '#fdf3dc'
canvas.fill_rect(0, 0, 1000, 1000)
canvas.line_width = 0.1
for polygon in voronoi_polygons:
    plot_spiral(canvas, spiral(polygon, N=300, fraction=0.1))
canvas

Así se ve:

textil 01010-00100

Y aquí otro del que perdí la semilla y configuración aunque el efecto me gustó:

textil 01010-00100

Hay otro detalle aleatorio que no he mencionado: los polígonos se pueden recorrer en el sentido de las manecillas del reloj o el opuesto. Dependiendo de como se defina, el diagrama luce ligeramente distinto.

En general, me gustaría tener un algoritmo decente (no necesariamente óptimo) que, dado un conjunto de puntos, calculara una teselación con polígonos convexos que usen los todos los puntos como vértices de tal forma que los polígonos tengan el mayor número de lados posible. No sé si exista una solución buena a ese problema. Tal vez busque después.